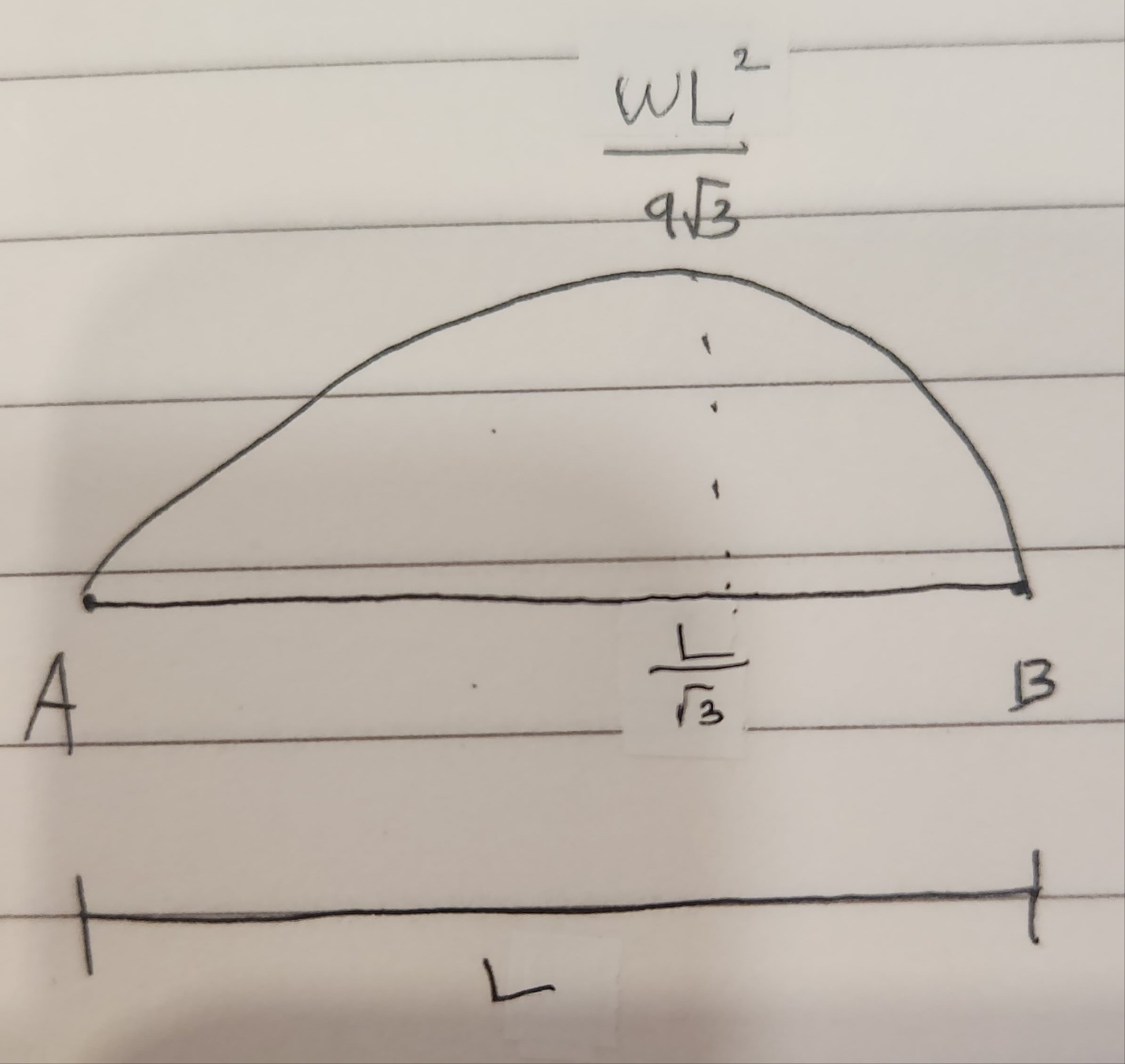
단순보에서 등변분포하중의 BMD는 위 그림처럼 3차함수의 형태로 나타내어진다고 배웠습니다.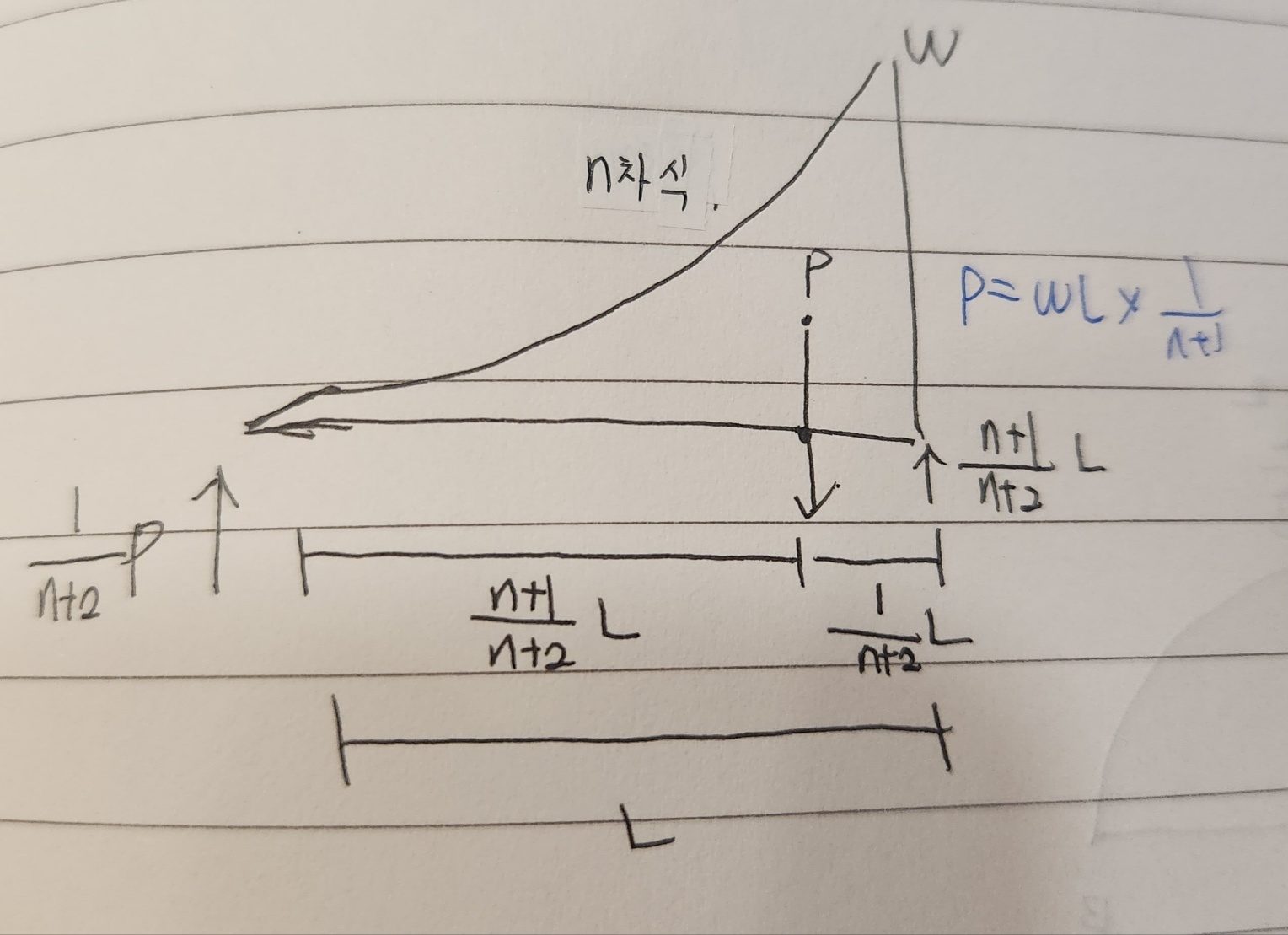

그리고 함수로 나타내어질때 n차식인 하중은 두번째 사진처럼 된다고 알고있습니다.

이제 제가 궁금한걸 여쭤보겠습니다. 기본적으로 분포하중을 다룰때는 두번째 사진처럼 아래로 볼록한 형태일때 도심도 찾고 집중하중도 구할수 있는데, 등변분포하중의 BMD는 위로 볼록한 3차함수고 올라갔다 내려가는 구간까지 있어서 어느 점에서 집중하중이 생기는지도 모르겠습니다. 그래서 당연히 A,B 지점에서 생기는 지점반력도 못 구하겠습니다.등분포하중이 가해질때는 BMD가 2차함수여서 지점반력도 구할수 있고, 공액보에서도 처짐,처짐각을 구할수 있었는데 등변분포하중의 BMD는 3차함수이고 거기에다 위로볼록한 형태라서 지점반력들과 공액보라고 가정했을때의 처짐,처짐각도 못 구하겠어서 질문 드립니다.