Message Board
[온라인강의] 공액보에 관해서 한번만 더 질문하겠습니다
김*우2025.01.26답변완료
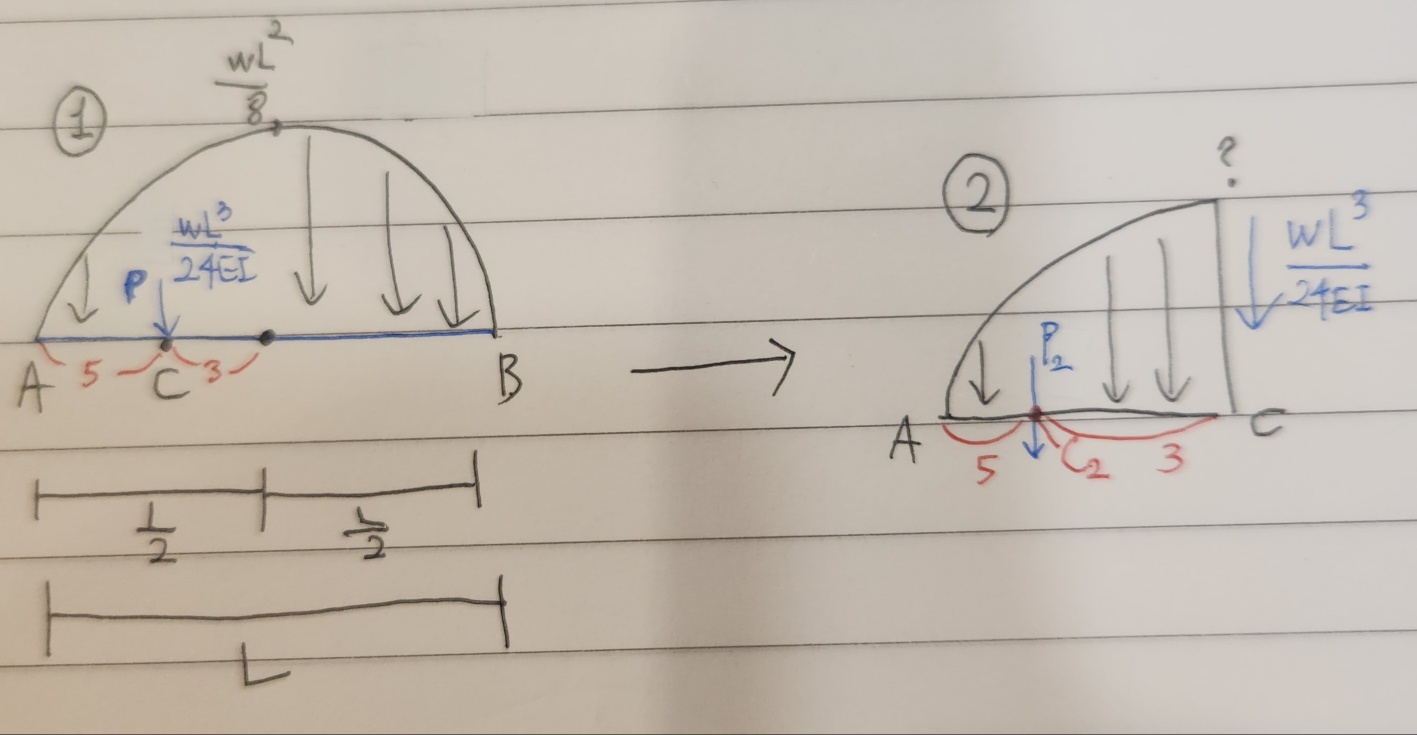
등분포하중의 BMD는 1번 그림처럼 2차함수 형태로 나타내어진다고 배웠습니다. 이것으로 공액보법을 사용한다고 했을때, A쪽의 처짐각을 구하기 위하여 ① 그림에서 P라는 하중이 C라는 지점에 작용한다고 배웠고, ② 그림은 C지점을 절단하여 왼쪽을 선택한 그림입니다. 이때 원래라면 절단된 그림에서 P₂라는 새로운 하중이 C₂ 지점에서 생긴다고 알고있는데 공액보법에서는 P₂가 생기지 않는다고 생각하여 처짐각과 처짐을 구하는게 맞나요?
답변안광호2025.01.31 11:11
안녕하세요,,,
새로운 하중이 생긴다라고 하는데, 그러한 것은 없습니다.
탄성하중도에 대한 면적을 집중하중으로 치환한 것이 도심에 작용할 때라고 생각을 변환시켜 주시기 바랍니다.
휨모멘트(M)도를 하중으로 바꾼 탄성하중도(M/EI)에서 지점반력을 구해놓습니다.
가상의 공액보상에서 특정의 위치 x에서 전단력을 구한 것은 실제의 보에서 x위치의 처짐각이 되고,
가상의 공액보상에서 특정의 위치 x에서 휨모멘트를 구한 것은 실제의 보에서 x위치의 처짐이 된다는 것이 공액보법의 이론입니다.
감사합니다.
TOP