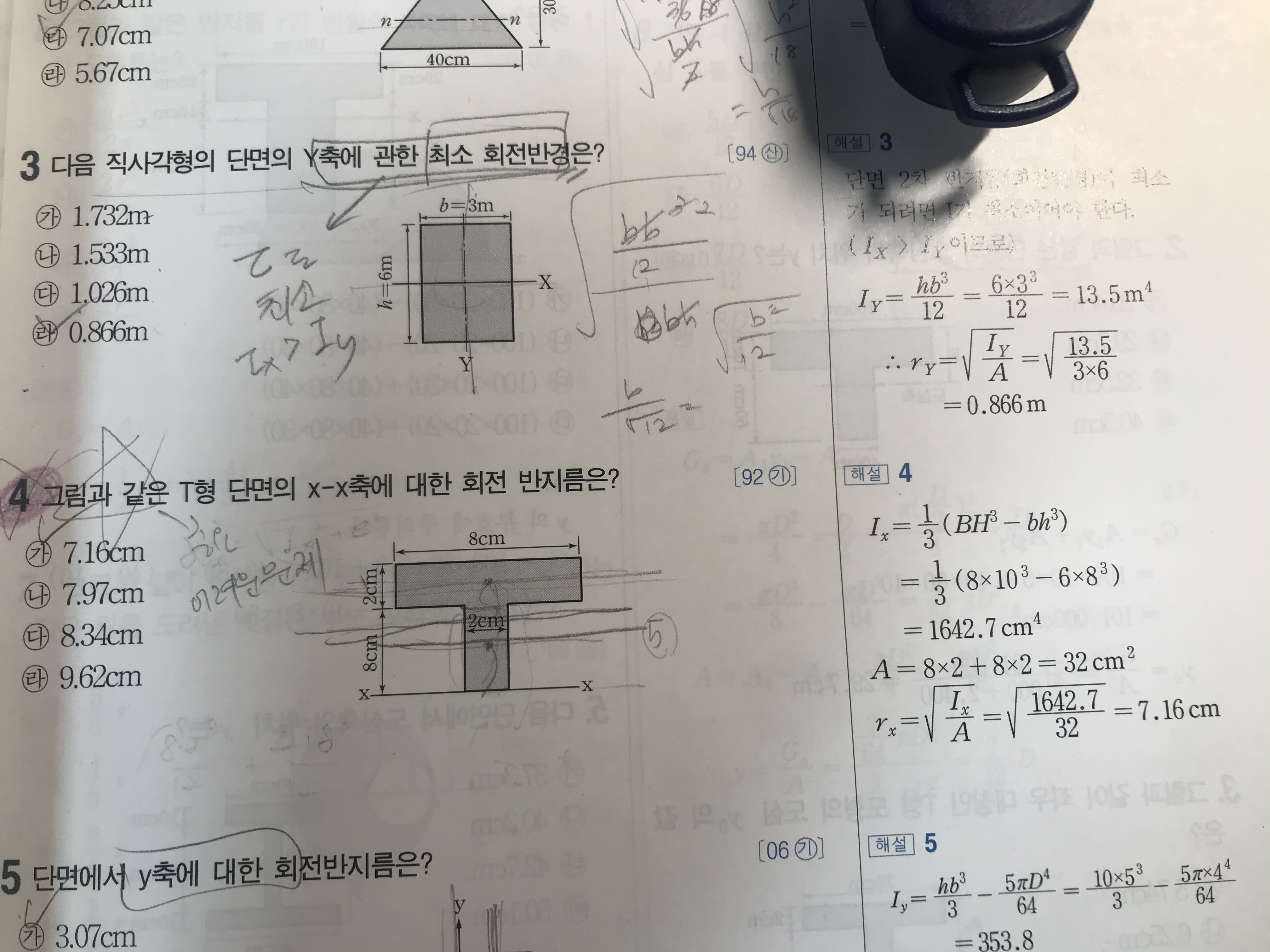
해당 4번 문제에서 회전반경을 구할때 x-x축으로 축이동한 단면이차모멘트를 구한 후 단면적으로 나눈 값의 제곱근을 구하였습니다. 

궁금증이 들어 시간이 더 걸리는 방법이지만 다른방법으로 풀어봤는데 답이 달라서요! 답이 0.14정도 다르지만 아래처럼 푼 방법도 맞는 해결법인지 궁금해서요!

단면일차모멘트를 단면적으로 나눠 도심(도심축)을 구하고, 해당 도심축에 대한 단면이차모멘트를 구한후(플렌지와 보 각 단면에서 이차모멘트구한후 도심축으로 축이동) , 축이동에 대한 단면 이차 반지름 공식을 이용해 풀었습니다!