안녕하세요? 안광호선생님

한솔 11년 6월 문제4번입니다.

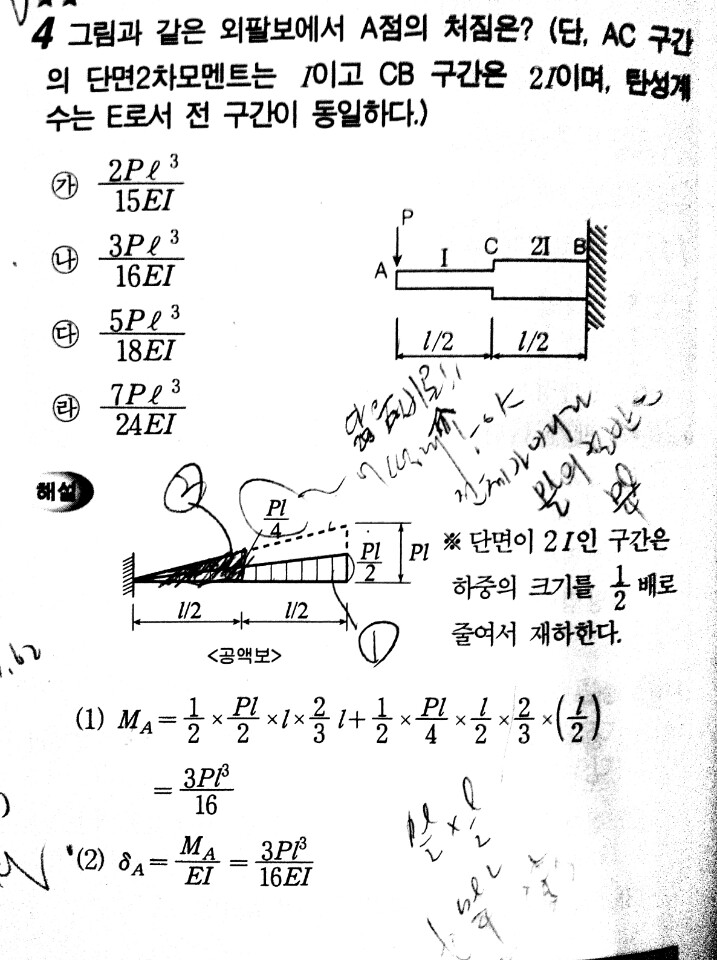
Ma=1/2×PL/2×L×(2/3×L) + 1/2×PL/4×L/2×2/3×L/2 = 3PL^3/16EI입니다.

공액보상에서 ①긴삼각형(밑변길이:L,높이:PL/2)과 ②짦은 삼각형(밑변길이:L/2,높이:PL/2->긴삼각형의 높이 아님)이 서로 겹치기 때문에 겹치는 부분(밑변길이:L/2,높이:PL/4,=밑변이 대각선이 아닌 직선인 삼각형)을 빼고, 각각의 삼각형의 면적인 변등분포하중을 집중하중으로 전환해서 A점의 처짐을 구해주어야한다고 생각합니다.

하지만, 해설에서 1/2×PL/4×L/2×2/3×L/2이 의문입니다.

②짦은 삼각형의 면적에서 ①긴삼각형과 겹치는 면적을 제외했을 때의 도형의 모양이 삼각형이 아닌데, "이 부분의 면적(②짧은삼각형에서 겹치지 않는 부분의 면적)"이 "겹치는 부분의 면적(밑변길이:L/2,높이:PL/4인 직각삼각형)"과 값이 미세하기 때문에 동일하게 생각해주어 1/2×PL/4×L/2×2/3×L/2의 공식이 만들어 지는지 궁금합니다.

감사합니다