안녕하세요,,,

19번 문제로 올려주신 그림은 고정단이 없는 연속보입니다.

수직하중이 작용할 때 A점과 C점에서 휨모멘트가 0일 것이라는 것과, B점에서 부(-)모멘트가 생긴다는 것은 쉽게 예측할 수 있습니다. 억지로 모멘트분배법을 적용하기보다는 교재의 364페이지의 3연모멘트방정식으로 아주 간명하게 처리할 수 있습니다.

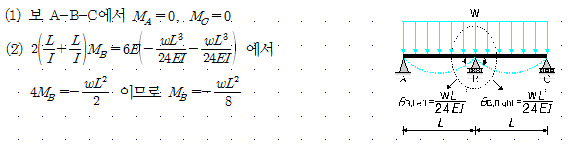
10번 문제는 A지점과 C지점 양쪽이 고정단인 것이 위의 문제와 다른 점임을 관찰하시고, 고정단이 있는 보나 라멘의 해석은 모멘트분배법이 적합한 방법이 됩니다.

이때 고정단모멘트라는 것이 AB부재 중간에 작용하는 수직하중에 의해 A쪽에서는 반시계, B쪽에서는 시계방향의 회전력이 발생합니다. BC부재 중간에 작용하는 수직하중에 대해서는 B점에서는 반시계, C점에서는 시계방향의 회전력이 발생하게 됩니다.

B지점을 중심으로 발생되는 회전력의 차이를 계산해놓고 A쪽과 C쪽의 강한정도(=강도계수)만큼 나누어갖는 형태로 해석을 시도하면 되겠습니다.

10번 문제와 같은 고정단이 있는 연속보를 억지로 3연모멘트법으로 해석하려면 굉장히 머리가 아픕니다.

19번 문제와 같은 고정단이 없는 연속보를 모멘트법으로 해석하려면 모멘트분배법의 고정단모멘트를 억지로 차용하고 강도계수를 수정강도계수를 적용해야 하는 문제점이 발생합니다.

산 정상에 올라가서 생선회를 찾지 않고, 바닷가에 놀러가서 육개장을 찾지 않는 것처럼 적합한 해법을 찾아 적용하는 것이 부정정구조의 해석에 기본이 되는 사항이라고 보시면 되겠습니다.

감사합니다.